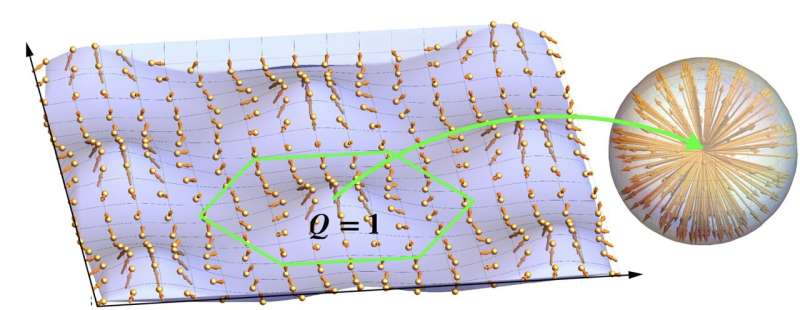
Image of a 'water-wave skyrmion' (i.e., a structure where the water-surface particles of certain area are displaced in all possible directions, mapped onto the sphere of directions) in the interference of three plane water waves with the same frequency and amplitude but different propagation directions. Credit: Smirnova et al
Topological wave structures are wave patterns that exhibit specific topological properties, or in other words, properties that remain unvaried under smooth deformations of a physical system. These structures, such as vortices and skyrmions, have attracted significant attention within the physics research community.
While physicists have carried out extensive studies focusing on topological wave structures in various wave systems, surprisingly their most classical example remains unexplored. These are water waves, oscillations or disturbances that propagate on the surface of water or other fluid.
Researchers at RIKEN recently set out to fill this gap in the literature, by offering a description of various water-wave topological structures. Their paper, published in Physical Review Letters, offers a theoretical framework that could inform future experiments aimed at emulating topological wave phenomena.
"I have been working on topologically nontrivial wave structures, such as wave vortices, skyrmions, etc., for almost 20 years," Konstantin Y. Bliokh, co-author of the paper, told Phys.org. "First, I focused on optical (electromagnetic) fields, then for quantum electron waves, and more recently for acoustic wave fields. Only recently I realized that such topological structures have not been systematically studied for the most obvious type of classical waves: water waves."
In their paper, Bliokh and his collaborators provide a theoretical description of four different types of topological wave structures. These include water-wave vortices carrying quantized angular momentum with orbital and spin contributions, skyrmion lattices and meron lattices formed on the surface of water, and spatiotemporal water-wave vortices and skyrmions.
"The main wave phenomena have a universal character for waves of different nature, both classical and quantum, because of the mathematical similarity of different wave equations," Bliokh explained. "In our case, we had to apply the analysis, previously developed to electromagnetic, acoustic and quantum-mechanical wave equations, to the equations describing linear waves (either gravity or capillary) on the water surface."
The recent work by this team of researchers shows that classical water waves can exhibit topologically nontrivial structures with interesting physical properties. The theoretical descriptions of these structures outlined in their paper could inform future studies and experimental efforts focusing on fluid mechanics.
"In the past decades, wave vortices have found numerous applications in optical, acoustic, and quantum systems," Bliokh said. "It is natural to expect that this will also happen in hydrodynamical systems. In particular, we expect that dynamical properties of water-wave vortices can be employed for microfluidic manipulation of small particles, including biomedical objects."
In addition to paving the way for new research exploring fluid mechanics, this recent paper shows that water waves could be a robust tool to model complex wave phenomena that are difficult to observe in other wave systems, such as quantum systems. Bliokh and his colleagues will now try to observe the structures that they theoretically described within laboratory settings.
"In our next studies, we plan to observe experimentally the water-wave structures (vortices, skyrmions, etc.), which were described theoretically in our work," Bliokh added. "We have already made good progress towards this goal."
More information: Daria A. Smirnova et al., Water-Wave Vortices and Skyrmions, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.054003. On arXiv: DOI: 10.48550/arxiv.2308.03520
Journal information: Physical Review Letters , arXiv
© 2024 Science X Network