Scientists propose theory of σ bond resonance in flat boron materials

Recently, two-dimensional (2D) boron sheets—borophenes—have drawn great interest from materials scientists because of their similarity to graphene. However, understanding of how the material can be stable in the 2D form is still lacking, mainly due to boron's unique electron-deficient nature.

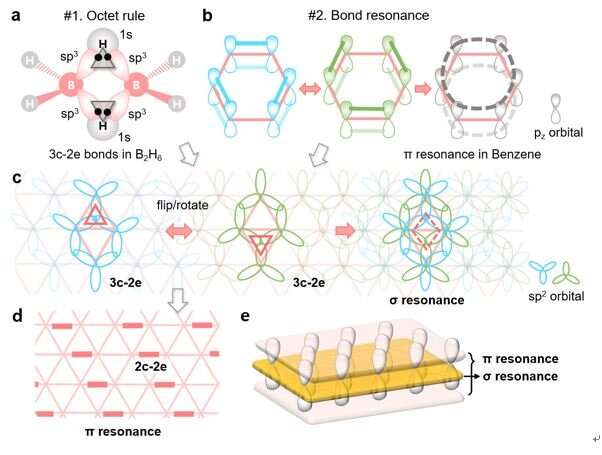
In chemistry, atoms in a stable material generally obey the octet rule. A carbon atom usually shares 8 electrons by forming 4 chemical bonds with its neighbors, specifically 3 σ and 1 π bonds for carbon atoms in graphene. While a boron atom has only 3 valence electrons, its stability, or its bonding strategy to have 8 electrons, has been a long-term mystery in history.

The concept of the three-center two-electron (3c-2e) bond allows us to understand how a boron atom satisfies the octet rule in boron-related small molecules, such as diborane (B₂H₆), and won the Nobel Prize in Chemistry in 1976. But, how boron atoms in complicated boron materials like borophenes obey the octet rule and maintain stable, is still beyond our knowledge.

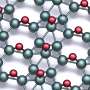
Additionally, in carbon materials like benzene, bond resonance or aromaticity could further stabilize the materials by delocalizing the π electrons, out of the plane, to a larger area. Could we extend the theory to the 2D boron sheet to explain its triangular lattice-based structure and stability?

Scientists from the Department of Materials Science and Engineering, and Mechanical Engineering at UNIST, in cooperation with researchers at Rice University, U.S., and Nankai University, China, proposed a new bonding theory, which solves the long-term mystery by illustrating both i) how each boron atom in a borophene satisfies the octet rule based on the unique 3c-2e bonds and ii) how the resonance of alternating 3c-2e σ bonds further stabilizes the 2D sheet in its triangular lattice.

Interestingly, this theory, in analogy to π resonance in carbon materials, introduces a new form of resonance, which allows the delocalization of σ electrons within the 2D plane. In combination with the out-of-plane π resonance, the triangular boron sheet in fact exhibits a sandwich electronic structure, composing of both in-plane and out-of-plane delocalized electrons.

Based on the theory, everyone can draw the bonding structures of these new boron materials, like drawing the Kekulé structures of the benzene molecule. Therefore, stability and properties of the borophene materials can be easily understood without performing complicated quantum calculations.

Major puzzles in the field, such as how hexagonal holes stabilize the triangular boron lattice, why neutral borophene with 1/9 hole ratio are energetically most favorable, and how substrate doping affects the hole concentration in borophene, are well explained for the first time. "The theory reveals the origin of the unique properties of these flat boron materials, and therefore offers an avenue for the controlled synthesis and design of borophene by predicting their stabilities on the substrates," noted the first author of the study, Dr. Lu Qiu.

Intuitive understanding of bonding in various molecules and materials is always the core part of chemistry. "Our theory, for the first time, provides fundamental and necessary elements for studying flat boron materials without performing any quantum calculations," says the corresponding author of the study, Prof. Feng Ding, "thus, we are confident that this σ bond resonance theory will further stimulate the community towards accelerating design and synthesis of boron related materials, like the aromaticity theory for carbon materials."

The work is published in the journal Nature Communications.