A new way to identify stresses in complex fluids

Fluid dynamics researchers use many techniques to study turbulent flows like ocean currents, or the swirling atmosphere of other planets. Arezoo Adrekani's team has discovered that a mathematical construct used in these fields provides valuable information about stress in complex flow geometries.

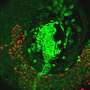
Ardekani, a Purdue University professor of mechanical engineering, studies complex flows: from the transport processes related to biopharmaceuticals, to the behavior of microorganisms around an oil spill. "Newtonian fluids like water are simple to understand, because they have no microstructure," she said. "But complex fluids have macromolecules that stretch and relax, and that changes many properties of the fluid, leading to very exciting fluid dynamics."

Viscoelastic flows occur frequently in nature, in biomedical settings, and in industrial applications—such as solutions used in groundwater remediation. "When groundwater becomes contaminated, remediators use certain polymer-based solutions to disperse chemicals designed to break down the contaminants," Ardekani said. "But what type of polymer should they use, how much, and where should they inject it? The only way to answer those questions is by understanding the behavior of these flows, which comes down to measuring stresses."

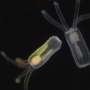
Currently, the only way to quantify the stresses of polymeric fluids is a technique called birefringence, which measure specific optical properties of the fluid. But it's very difficult to perform, often inaccurate, and doesn't apply to all types of macromolecules.

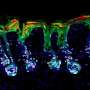
Ardekani's team has discovered a new technique. The researchers created a mathematical framework that takes input from flow velocity, obtained from particle image velocimetry (a common technique in fluid dynamics), and outputs stress and stretching field topologies for complex fluids. Their research has been featured in Proceedings of the National Academy of Sciences (PNAS).

In particle image velocimetry (PIV), tracer particles are injected into a fluid. By using the movement of those particles, researchers can extrapolate information about the overall flow kinematics. While this can be readily used to evaluate stress in Newtonian fluids, Ardekani's team has discovered a mathematical correlation between these measurements and the stresses in viscoelastic flows.

It all connects through something called Lagrangian coherent structures (LCSs). "Lagrangian coherent structures are mathematical constructs used to predict the dynamics of fluid flows," Ardekani said. "They are used by oceanographers to predict how currents will move; biologists who are tracking microorganisms; and even astrophysicists, who are observing the turbulent clouds on places like Jupiter."

While LCSs are often used by turbulence researchers, they have never been applied to polymeric stress until now. "We have united two disparate branches of continuum mechanics," Ardekani said. "Using Lagrangian stretching, and applying it to Eulerian stress fields. And this applies to a wide range of scales, from the mesoscale all the way up to industry scale measurements."

The paper is a collaboration between Ardekani, her Ph.D. student Manish Kumar and Jeffrey Guasto, Associate Professor of Mechanical Engineering at Tufts University. They presented their findings in November at the 75th Annual Meeting of the APS (American Physical Society) Division of Fluid Dynamics in Indianapolis, which Ardekani co-organized.

While the research is largely mathematical, Ardekani is excited to see how experimentalists will use the technique in the lab and in the real world. "Let's use our groundwater remediation example again," Ardekani said. "Researchers typically use tracer analysis on the injected fluids to measure the velocity field. But now, they can also identify the stress fields, so they can more accurately predict the transport of that fluid."