New political redistricting procedure may prevent gerrymandering by forcing parties to act fairly

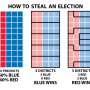
Voting districts are redrawn following each census in the United States. In most states, new district maps are implemented by the state legislature. This makes the process prone to manipulation by the current majority party, or gerrymandering. Although the Supreme Court has ruled that gerrymandering violates the Fourteenth Amendment, it has not established criteria to evaluate cases, making the practice difficult to identify and correct.

Researchers with the Institute for Computational Redistricting at the University of Illinois Urbana-Champaign have proposed an alternative redistricting procedure in their article "A Bisection Protocol for Political Redistricting" published in the INFORMS Journal on Optimization. Their bisection protocol takes input from two major political parties and results in quantifiably fairer district maps by several common metrics.

The bisection protocol begins with one party dividing the state into two halves of equal population. The other party then divides each of those pieces in half. Parties continue dividing the resulting pieces until the required number of districts is reached.

According to the article's lead author Ian Ludden, the bisection protocol draws inspiration from the "I cut, you choose" method of fair cake cutting.

"If you and I wanted to split a piece of cake fairly," he said, "you could cut it into two pieces, and then I could pick which piece I want. That protocol gives us a fair way of sharing a cake where neither of us wishes we had the other person's piece. Our work adapts that idea to political redistricting."

Ludden and co-authors Rahul Swamy, Douglas King, and Sheldon Jacobson found the bisection protocol can lead to fairer maps than when one party controls the whole redistricting process. They analyze bisection using techniques from game theory, a field of mathematics concerned with evaluating decision strategies, to prove the bisection protocol has a strategic equilibrium where no player can benefit from switching strategies.

The optimal high-level strategy for both parties is dividing each piece to group as many party voters together as possible. Such a "packing" strategy implicitly packs opposition voters into the other pieces and precludes "cracking," a form of gerrymandering that dilutes voters across districts.

While the researchers' equilibrium proof is in the idealized setting of a state with a continuously divisible population that allows non-contiguous districts, the packing strategy yielded promising results when the bisection protocol was applied to states with four to eight districts. In a case study of Iowa, the bisection-produced district plan was comparable to or fairer than the actual map. Fairness was quantified with several common metrics like efficiency gap and partisan symmetry.

The bisection protocol has another advantage when compared to other proposals for fair-by-design redistricting procedures: it is more efficient to implement.

Encouraged by the bisection protocol's efficiency and fairness, the researchers are exploring more complex strategies for real state geographies. They are also considering how to reduce the advantage given to the first party.

Jacobson, the director of the Institute for Computational Redistricting and a professor of computer science, noted that the bisection protocol is one of many methods drawing from political science, computer science, and game theory that institute researchers are developing. "Redistricting is viewed as a political problem," he said, "but we believe the solution is going to be computational."

He added that the institute approaches redistricting from a nonpartisan perspective, saying "All we're trying to do is expose the nefariousness of gerrymandering and provide computational tools to facilitate transparent redistricting."